Code

快排

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19


public static void quickSort(int a, int l, int r) {
    if(l >= r) return ;
    int x = a[l + r >> 1], i = l - 1, j = r + 1;
    while(i < j) {
        while(a[++i] < x) ;
        while(a[--j] > x) ;
        if(i < j) {
            int t = a[i];
            a[i] = a[j];
            a[j] = t;
        }
    }
    quickSort(1, j);
    quickSort(j + 1, r);
    /*
    quickSort(1, i - 1);
    quickSort(i, r);
    */
}

归并

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19


public static void mergeSort(int a, int l, int r) {
    if(l >= r) return ;
    
    int mid = l + r >> 1;  // l + (r - l) / 2
    mergeSort(l, mid);
    mergeSort(mid + 1, r);
    
    int k = 0, i = l, j = mid + 1;
    while(i <= mid && j <= r) {
        if(a[i] <= a[j]) temp[k++] = temp[i++];
        else temp[k++] = temp[j++];
    }
    while(i <= mid) temp[k++] = a[i++];
    while(j <= r) temp[k++] = a[j++];
    
    for(int i = l, j = 0; i <= r; i++, j++) {
        a[i] = temp[j];
    }
}

冒泡

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28


public static void BubbleSort(int a, int n) {
    for(int i = 0; i < n; i++) {
        for(int j = 1; j < n - i; j++) {
            if(a[j - 1] > a[j]) {
                int t = a[j - 1];
                a[j - 1] = a[j];
                a[j] = t;
            }
        }
    }
}

// 优化
public static void BubbleSort(int a, int n) {
    for(int i = 0; i < n; i++) {
        int exchange = 0;
        for(int j = 1; j < n - i; j++) {
            if(a[j - 1] > a[j]) {
                int t = a[j - 1];
                a[j - 1] = a[j];
                a[j] = t;
                
                exchange = 1;
            }
        }
        if(exchange == 0) break;  // 代表已经有序
    }
}

二分

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21


// 寻找x

int l = 0, r = n - 1;

// 左边界
while(l < r) {
    int mid = l + r >> 1;
    if(a[mid] >= x) r = mid;
    else l = mid + 1;
}

// 右边界
int l = 0, r = n - 1;
while(l < r) {
    int mid = l + r + 1 >> 1;
    if(a[mid] <= x) l = mid;
    else r = mid - 1;
}

// 加=表示寻找小于等于mid的最后一个元素
// 不加=表示寻找小于mid的最后一个元素

BigInteger

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20


public BigInteger(String val)
	add
    subtract
    multiply
    divide
    mod / remainder
    max
    min
    divideAndRemainder // 返回一个数组[商, 余数]
    
BigInteger bi1 = new BigInteger("61893691328915");
BigInteger bi2 = new BigInteger("1234354654424");
bi2.add(bi1);
bi2.subtract(bi1);
bi2.multiply(bi1);
bi2.divide(bi1);
bi2.mod(bi1);
bi2.max(bi1);
bi2.min(bi1);
bi2.divideAndRemainder(bi1);

BigDecimal

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12


public BigDecimal(double val)
public BigDecimal(int val)
public BigDecimal(String val)
    add
    subtract
    multiply
    divide
    
// BigDecimal转double
double b = b1.add(b2).doubleValue();
// 四舍五入
b1.divide(b2, len, BigDecimal.ROUND_HALF_UP);

前缀和

1
2
3
4
5
6
7


// 一维前缀和
S[i] = S[i - 1] + a[i];  // 下标从1开始
a[l ... r] = S[r] - S[l - 1];

// 二维前缀和
S[i][j] = S[i - 1][j] + S[i][j - 1] - S[i - 1][j - 1] + a[i][j];
a[x1..x2][y1..y2] = S[x2][y2] - S[x1-1][y2] - S[x2][y1-1] + S[x1-1][y1-1];

差分

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21


/*
初始:
前缀和: 0 0 0 0 0
差分: 0 0 0 0 0
*/

public static void insert(int l, int r, int c) {
    a[l] += c;
    if(r < n) a[r + 1] -= c; // 下标从1开始
}

/*
二维差分
*/

public static void insert(int l1, int r1, int l2, int r2, int c) {
    b[l1][r1] += c;
    if(l2 < n) b[l2 + 1][r1] -= c;
    if(r2 < m) b[l1][r2 + 1] -= c;
    if(l2 < n && r2 < m) b[l2 + 1][r2 + 1] += c;
}

双指针

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11


// 暴力 --- 优化
/*
暴力：o(n^2)
优化：o(n) / o(logn) / o(nlogn)
*/

for(int i = 0, j = 0; i < n; i++) {
    while(j <= i && check(i, j)) {
        // ...
    }
}

位运算

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16


/*
求n的低=第k位数：(n >> k) & 1
返回n的最后一位1：x & -x
lowbit：截取数字中最后一个1后面的所有位
*/

// 计算1的个数
public static int lowbit(int x) {
    int cnt = 0;
    while(x > 0) {
        int t = x & (-x);
        x -= t;
        cnt++;
    }
    return cnt;
}

离散化

1
2
3
4
5
6
7


/*
list通过流去重排序
import java.util.stream.Collectors;
list = list.stream().distinct().sorted().collect(Collectors.toList());
*/

// 映射采用二分，暴力会超时

区间合并

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22


/*
想清楚情况：
i: |------|
     |--|
       |-----|
               |-----|

*/
// 依据左端点排序
Arrays.sort(arr, (a, b) -> a[0] - b[0]);
// 计算
int l = a[0][0], r = a[0][1];
for(int i = 1; i < n; i++) {
    if(a[i][0] > r) {
        list.add(new int[]{l, r});
        l = a[i][0];
        r = a[i][1];
    }else {
        r = Math.max(r, a[i][1]);
    }
}
list.add(new int[]{l, r});

链表

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33


// 单链表

public static void addHead(int x) {
    e[idx] = x;
    ne[idx] = h;
    h = idx++;
}

public static void add(int k, int x) {
    e[idx] = x;
    ne[idx] = ne[k];
    ne[k] = idx++;
}

public static void delete(int k) {
    ne[k] = ne[ne[k]];
}


// 双链表

public static void add(int k, int x) {
	    e[idx] = x;
	    r[idx] = r[k];
	    l[idx] = k;
	    l[r[idx]] = idx;
	    r[k] = idx++;
	}
	
	public static void delete(int k) {
	    r[l[k]] = r[k];
	    l[r[k]] = l[k];
	}

栈和队列

单调栈和单调队列

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12


// 单调队列
int[] q = new int[n];
int h = 0, t = -1;
for(int i = 0; i < n; i++) {
    // 队头是否移出
    if(h <= t && i - k + 1 > q[h]) h++;
    while(h <= t && a[q[t]] >= a[i]) t--;
    q[++t] = i;
    if(i >= k - 1) {
        bw.write(a[q[h]] + " ");
    }
}

KMP

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44


// 从0开始（不推荐）
// next
int[] next = new int[n];
next[0] = 0;
for(int i = 1, j = 0; i < n; i++) {
	while(j > 0 && p[i] != p[j]) j = next[j - 1];
	if(p[i] == p[j]) j++;
	next[i] = j; // 此时的j是可以匹配的或者0
}

// kmp
for(int i = 0, j = 0; i < m; i++) {
	while(j > 0 && s[i] != p[j]) {
		j = next[j - 1];
	}
	if(s[i] == p[j]) j++;
	if(j == n) {
		bw.write(i - n + 1 + " ");
		j = next[j - 1];
	}
}

// 从1开始
// next
int[] ne = new int[n + 1];
ne[1] = 0;
for(int i = 2, j = 0; i <= n; i++) {
	while(j > 0 && p[i] != p[j + 1]) j = ne[j];
	if(p[i] == p[j + 1]) j++;
	ne[i] = j; // 此时的j是可以匹配的或者0
}

// kmp
for(int i = 1, j = 0; i <= m; i++) {
	// 匹配失败，j后退
	while(j > 0 && s[i] != p[j + 1]) j = ne[j];
	// 匹配下一个
	if(s[i] == p[j + 1]) j++;
	// 匹配成功
	if(j == n) {
		bw.write(i - n + " ");
		j = ne[j];
	}
}

Tire

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19


public static void insert(String s) {
    int p = 1;
    for(int i = 0; i < s.length(); i++) {
        int x = s.charAt(i) - 'a' + 1;
        if(son[p][x] == 0) son[p][x] = ++idx;
        p = son[p][x];
    }
    cnt[p] ++;
}

public static int query(String s) {
    int p = 1;
    for(int i = 0; i < s.length(); i++) {
        int x = s.charAt(i) - 'a' + 1;
        if(son[p][x] == 0) return 0;
        p = son[p][x];
    }
    return cnt[p];
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41


class Trie {
    private Trie[] son;
    private boolean isEnd;

    public Trie() {
        son = new Trie[26];
        isEnd = false;
    }
    
    public void insert(String word) {
        Trie p = this;
        for(int i = 0; i < word.length(); i++) {
            int idx = word.charAt(i) - 'a';
            if(p.son[idx] == null) {
                p.son[idx] = new Trie();
            }
            p = p.son[idx];
        }
        p.isEnd = true;
    }
    
    public boolean search(String word) {
        Trie p = searchWord(word);
        return p == null ? false : p.isEnd;
    }
    
    public boolean startsWith(String prefix) {
        Trie p = searchWord(prefix);
        return p != null;
    }

    public Trie searchWord(String s) {
        Trie p = this;
        for(int i = 0; i < s.length(); i++) {
            int idx = s.charAt(i) - 'a';
            if(p.son[idx] == null) return null;
            p = p.son[idx];
        }
        return p;
    }
}

并查集

1
2
3
4


public static int find(int x) {
    if(p[x] != x) p[x] = find(p[x]);
    return p[x];
}

堆

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33


public static void swap(int i, int j) {
    // 1.交换ph指针
    int t = ph[hp[i]];
    ph[hp[i]] = ph[hp[j]];
    ph[hp[j]] = t;

    // 2.交换hp指针
    t = hp[i];
    hp[i] = hp[j];
    hp[j] = t;

    // 3.交换值
    t = a[i];
    a[i] = a[j];
    a[j] = t;
}

public static void down(int k) {
    int t = k;
    if(2 * k <= size && a[2 * k] < a[t]) t = 2 * k;
    if(2 * k + 1 <= size && a[2 * k + 1] < a[t]) t = 2 * k + 1;
    if(k != t) {
        swap(k, t);
        down(t);
    }
}

public static void up(int k) {
    while(k / 2 > 0 && a[k / 2] > a[k]) {
        swap(k / 2, k);
        k /= 2;
    }
}

哈希表

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25


// 开发寻址
public static int find(int x) {
    int k = (x % N + N) % N;
    while(h[k] != NULL && h[k] != x) {
        k++;
        if(k == N) k = 0;
    }
    return k;
}

// 拉链法
public static void insert(int x) {
    int n = (x % N + N) % N;  // 求非负余数而非余数取正，故不是abs
    // 头插法
    e[idx] = x; ne[idx] = h[n]; h[n] = idx++;

}

public static boolean query(int x) {
    int n = (x % N + N) % N;
    for(int i = h[n]; i != -1; i = ne[i]) {
        if(e[i] == x) return true;
    }
    return false;
}

DFS

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14


public void dfs(int k) {
    if(k == n) {
        // ...
    }
    
    for(int i = 1; i <= n; i++) {
        if(!st[i]) {
            // g[k] = i;
            st[i] = true;
            dfs(k + 1); // 前后恢复现场
            st[i] = false;
        }
    }
}

BFS

1
2
3
4
5
6
7
8


public int bfs(int k) {
    Queue<Integer> q = new LinkedList<>();
    // 初始化...
    while(!q.isEmpty()) {
        int t = q.poll();
        // 拓展t...
    }
}

深度优先遍历

 1
 2
 3
 4
 5
 6
 7
 8
 9
10


public int dfs(int k) {
    st[k] = true;
    for(int i = h[k]; i != -1; i = ne[i]) {
        int j = e[i];
        if(!st[j]) {
            // ...
            dfs(j);
        }
    }
}

广度优先遍历

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16


public int bfs() {
    Queue<Integer> q = new LinkedList<>();
    q.offer(1);
    d[1] = 0; /* st[1] = true; */
    while(!q.isEmpty()) {
        int t = q.poll();
        for(int i = h[t]; i != -1; i = ne[i]) {
            int j = e[i];
            if(d[j] == -1 /* !st[j] */) {
                d[j] = d[t] + 1; /* st[j] = true; */
                q.offer(j);
            }
        }
    }
    return d[n];
}

拓扑排序

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24


public boolean topSort() {
    Queue<Integer> q = new LinkedList<>();
    // 将所有入度为0的点加入队列
    for(int i = 1; i<= n; i++) {
        // d[i] 表示i节点的入度有几个
        if(d[i] == 0) {
            q.offer(i);
        }
    }
    
    while(!q.isEmpty()) {
        int t = q.poll();
        g[cnt++] = t;
        for(int i = h[t]; i != -1; i = ne[i]) {
            int j = e[i];
            d[j]--; // 先删去当前的关系，不为0说明还有其他点指向当前的点
            if(d[j] == 0) {
                q.offer(j);
            }
        }
    }
    // 所有点都进入结果数组了，说明存在；否则不存在
    return cnt == n;
}

Dijkstra

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22


public int dijkstra() {
    Arrays.fill(d, INF);
    d[0] = 1;
    // 遍历n次，每次加入一个点
    for(int i = 0; i < n; i++) {
        // 1.找到S中不存在且距离最短的点t
        int t = -1;
        for(int j = 1; j <= n; j++) {
            if(!st[j] && (t == -1 || d[t] > d[j])) {
                t = j;
            }
        }
        // 2.将t加入S中
        st[t] = true;
        // 3.通过t更新其他点到起点的距离
        for(int j = 1; j <= n; j++) {
            d[j] = Math.min(d[j], d[t] + g[t][j]);
        }
    }
    // 返回结果，若为INF表示无法达到
    return d[n] == INF ? -1 : d[n];
}

Bellman-ford

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23


class Edge {
    int a, int b, int w;
    public Edge(int a, int b, int w) {
        this.a = a;
        this.b = b;
        this.w = w;
    }
}

public static int bellmanFord() {
    Arrays.fill(d, INF);
    d[1] = 0;
    for(int i = 0; i < k / n; i++) {
        db = Arrays.copyOf(d, N); // 备份，防止串联修改
        for(int j = 0; j < m; j++) { // 遍历所有边
            int a = edges[j].a, b = edges[j].b, w = edges[j].w;
            d[b] = Math.min(d[b], db[a] + w);
        }
    }
    return d[n] > INF / 2 ? -1 : d[n];
}

// INF / 2

Spfa

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22


public int spfa() {
    Queue<Integer> q = new LinkedList<>();
    q.offer(1);
    Arrays.fill(d, INF);
    d[1] = 0;
    st[1] = true; // 判断点是否在队列中
    while(!q.isEmpty()) {
        int t = q.poll();
        st[t] = false;
        for(int i = h[t]; i != -1; i = ne[i]) {
            int j = e[i];
            if(d[j] > d[t] + w[i]) { // 只有当d[t]减小时，d[j]才有可能减小
                d[j] = d[t] + w[i];
                if(!st[j]) {
                    st[j] = true;
                    q.offer(j);
                }
            }
        }
    }
    return d[n] > INF ? -1 : d[n];
}

Floyd

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19


// 初始化
for(int i = 1; i <= n; i++) {
    for(int j = 1; j<= n; j++) {
        if(i == j) d[i][j] = 0;
        else d[i][j] = INF;
    }
}

public void floyd() {
    for(int k = 1; k <= n; k++) {
        for(int i = 1; i <= n; i++) {
        	for(int j = 1; j <= n; j++) {
                d[i][j] = Math.min(d[i][j], d[i][k] + d[k][j]);
            }
    	}
    }
}

// INF / 2

Prim

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21


public int prim() {
    Arrays.fill(d, INF);
    for(int i = 0; i < n; i++) {
        // 找到不在s中且距离最近的点
        int t = -1;
        for(int j = 1; j <= n; j++) {
            if(!st[j] && (t == -1 || d[j] < d[t])) {
                t = j;
            }
        }
        // 判断是否有连通
        if(i != 0 && d[t] = INF) return INF;
        if(i != 0) res += d[t];
        // 加入点
        st[t] = true;
        // 根据点修改其他点到集合的距离
        for(int j = 1; j <= n; j++) {
            d[j] = Math.min(d[j], g[t][j]);
        }
    }
}

Kruskal

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28


class Edge {
    int u, int v, int w;
    public Edge(int u, int v, int w) {
        this.u = u;
        this.v = v;
        this.w = w;
    }
}

public int kruskal() {
    // 将所有边按照权重升序
    Arrays.sort(edges, (a, b) -> a.w - b.w);
    // 枚举每条边，没连通加入
    for(int i = 0; i < n; i++) {
        int u = edges[i].u, v = edges[i].v, w = edges[i].w;
        int fu = find(u), fv = find(fv);
        if(fu != fv) {
            p[fu] = fv;
            res += w;
            cnt++;
        }
    }
    // 确保连通
    if(cnt < n - 1) return -1;
    else return res;
}

// 并查集的find函数

染色法

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23


// dfs or bfs

for(int i = 1; i <= n; i++) {
    if(color[i] == 0) {
        if(!dfs(i, 1)) {
            flag = false;
            break;
        }
    }
}
if(flag) ...;
else ...;

public static boolean dfs(int k, int c) {
    color[k] = c;
    for(int i = h[k]; i != -1; i = ne[i]) {
        int j = e[i];
        if(color[j] == 0) {
            if(!dfs(j, 3 - c)) return false;
        }else if(color[j] == c) return false;
    }
    return true;
}

匈牙利算法

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20


// 邻接表 or 邻接绝阵

for(int i = 1; i <= n1; i++) {
    Arrays.fill(st, false);
    if(find(i)) res++;
}

public boolean find(int k) {
    for(int i = h[k]; i != -1; i = ne[i]) {
        int j = e[i];
        if(!st[j]) {
            st[j] = true;
            if(match[j] == 0 || find(match(j))) {
                match[j] = k;
                return true;
            }
        }
    }
    return false;
}

数学知识

欧拉函数

1~N中与N互质的数的个数被称为欧拉函数，记为ϕ(N)

若在算数基本定理中，N = p1^a1^p2^a2^ … pm^am^
$$ ϕ(N) = N * \frac{p_1 - 1}{p_1} * \frac{p_2 - 1}{p_2} * ... * \frac{p_m - 1}{p_m} $$
乘法逆元

若整数 b，m 互质，并且对于任意的整数 a，如果满足 b|a，则存在一个整数 x，使得 a / b = a * x (mod m)

则称 x 为 b 的模 m 乘法逆元，记为b^-1^ (mod m)

b 存在乘法逆元的充要条件是 b 与模数 m 互质。当模数m为质数时，b^m-2^ 即为 b 的乘法逆元
欧几里得算法

gcd
费马小定理

如果p是一个质数，而整数a不是p的倍数，则有
$$ a^{p - 1} \equiv 1 \ (mod \ p) $$
裴蜀定理 —> 扩展欧几里得算法

对于任意正整数 a，b，一定存在非零整数 x，y 使得 ax + by = (a, b) （a，b的最大公约数）

ax0 + by0 = d

通解：
$$ \begin{cases} x = x_0 - k * \frac{b}{d} \\ y = y_0 + k * \frac{a}{d} \end{cases} $$
中国剩余定理

设正整数 m1，m2 … ，mk，两两互质，则同余方程组：
$$ \begin{cases} x \equiv a_1 \ (\ mod \ m_1 \ ) \\ x \equiv a_2 \ (\ mod \ m_2 \ ) \\ ... \\ x \equiv a_k \ (\ mod \ m_k \ ) \end{cases} $$
有整数解，并且在模 M = m1 * m2 * … * mk 下的解是唯一的，解为
$$ x \equiv (a_1M_1M_1^{-1} + a_2M_2M_2^{-1} + \ ... \ + a_kM_kM_k^{-1}) \ mod \ M $$
其中Mi = M / mi，Mi^-1^ 表示 Mi 模 mi 的逆元

扩展欧几里得算法

质数

判断质数

1
2
3
4
5
6
7


public boolean isPrime(int x) {
    if(x <= 1) return false;
    for(int i = 2; i <= x / i; i++) {
        if(x % i == 0) return false;
    }
    return true;
}

分解质因数

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14


public void divide(int x) {
    for(int i = 2; i <= x / i; i++) {
        if(x % i == 0) {
            int t = 0;
            while(x % i == 0) {
                t++;
                x /= i;
            }
            System.out.println(i + " " + t);
        }
        if(m > 1) System.out.println(m + " " + 1);
        System.out.println("");
    }
}

筛质数

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32


// 朴素法
// 会重复筛
public int getPrimes(int n) {
    int cnt = 0;
    int[] primes = new int[n + 1];
    boolean[] st = new boolean[n + 1];
    for(int i = 2; i <= n; i++) {
        if(!st[i]) {
            st[i] = true;
            primes[cnt++] = i;
            for(int j = i + i; j <= n; j += i) {
                st[j] = true;
            }
        }
    }
    return cnt;
}

// 线性法
public int getPrimes(int n) {
    int cnt = 0;
    int[] primes = new int[n + 1];
    boolean[] st = new boolean[n + 1];
    for(int i = 2; i <= n; i++) {
        if(!st[i]) primes[cnt++] = i;
        for(int j = 0; primes[j] <= n / i; j++) {
            st[primes[j] * i] = true;
            if(i % primes[j] == 0) break;
        }
    }
    return cnt;
}

约数

求约数

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13


public List<Integer> getDivisors(int x) {
    List<Integer> list = new ArrayList<>();
    for(int i = 0; i <= m / i; i++) {
        if(m % i == 0) {
            list.add(i);
        }
        // 去重
        if(i != m / i) list.add(m / i);
    }
    // 排序
    list.sort(Comparator.naturalOrder());
    return list;
}

约束个数 & 约束之和

N = p1^a1^ * p2^a2^ * … * pk^ak^

约数个数：(a1 + 1) * (a2 + 1) * … * (ak + 1)

约数之和：(p1^0^ + p1^1^ + … + p1^a1^) * (p2^0^ + p2^1^ + … + p2^a2^) * … * (pk^0^ + pk^1^ + … + pk^ak^)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15


Map<Integer, Integer> map = new HashMap<>();
for(int i = 0; i < n; i++) {
    int m = Integer.parseInt(br.readLine());
    for(int j = 2; j <= m / j; j++) {
        if(m % j == 0) {
            int t = 0;
            while(m % j == 0) {
                t++;
                m /= j;
            }
            map.put(j, map.getOrDefault(j, 0) + t);
        }
    }
    if(m > 1) map.put(m, map.getOrDefault(m, 0) + 1);
}

最大公约数（欧几里得算法 / 辗转相除法）

1
2
3
4


// a > b
public int gcd(int a, int b) {
    return b == 0 ? a : gcd(b, a % b);
}

欧拉函数

1
2
3
4
5
6
7
8
9


long res = n;
for(int i = 2; i <= n / i; i++) {
    if(m % i == 0) {
        res = res / i * (i - 1);
        while(m % j == 0) m /= j;
    }
    
    if(m > 1) res = res / m * (m - 1);
}

快速幂

 1
 2
 3
 4
 5
 6
 7
 8
 9
10


// a^b
public long qmi(int a, int b) {
    long res = 1;
    while(b > 0) {
        if((b & 1) == 1) res *= a;
        a *= a;
        b >> 1;
    }
    return res;
}

扩展欧几里得算法

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14


// 求 x, y
// a * x + b * y = gcd(a, b)
public int exgcd(int a, int b, int[] result) {
    if(b == 0) {
        result[0] = 1;
        result[1] = 0;
        return a;
    }
    int d = exgcd(b, a % b, result);
    int t = result[0];
    result[0] = result[1];
    result[1] = t - a / b * result[1];
    return d;
}

中国剩余定理

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50


import java.util.*;
import java.io.*;

public class Main {
	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		int n = Integer.parseInt(br.readLine());
        String[] s = br.readLine().split(" ");
        long a1 = Integer.parseInt(s[0]);
        long m1 = Integer.parseInt(s[1]);
        // 用于标记是否有解，初始化为 true
        boolean hasAnswer = true;
		while(n-- > 1) {
		    s = br.readLine().split(" ");
            long a2 = Integer.parseInt(s[0]);
            long m2 = Integer.parseInt(s[1]);
            long[] result = new long[2];
            long d = exgcd(a1, a2, result);
            if((m2 - m1) % d != 0) {
                hasAnswer = false;
                break;
            }
            
            result[0] *= (m2 - m1) / d;
            long t = a2 / d;
            result[0] = (result[0] % t + t) % t;
            
            m1 = result[0] * a1 + m1;
            a1 = Math.abs(a1 / d * a2);
		}
		if(hasAnswer) {
		    System.out.println((m1 % a1 + a1) % a1);
		}else {
		    System.out.println("-1");
		}
	}
	
	public static long exgcd(long a, long b, long[] result) {
	    if(b == 0) {
	        result[0] = 1;
	        result[1] = 0;
	        return a;
	    }
	    long d = exgcd(b, a % b, result);
	    long t = result[0];
	    result[0] = result[1];
	    result[1] = t - a / b * result[1];
	    return d;
	}
}

高斯消元

求组合数

1
2
3
4
5
6
7
8
9


// 从 a 个苹果中选 b 个苹果
// 从 i 个苹果中选 j 个苹果
int c[N][N];
public void init() {
    for (int i = 0; i < N; i++)
        for (int j = 0; j <= i; j++)
            if (j == 0) c[i][j] = 1;
            else c[i][j] = (c[i - 1][j] + c[i - 1][j - 1]) % mod;
}

容斥原理

博弈论

数据结构

String：字符串

String s = “aabccabcd”

s.charAt(2); // ‘b’
s.concat(“hello”); // “aabccabcdhello”
s.startsWith(“hello”); // 判断字符是否以"hello"开头
s.endsWith(“hello”); // 判断字符是否以"hello"结尾
s.equals(“aaaaa”); // 判断字符串是否相等
s.equalsIgnoreCase(“aaaa”); // 忽略大小写比较是否相等
s.getBytes(); // 将字符串转化为字节数组
s.length(); // 返回此字符串的长度
s.replace(‘a’, ‘f’); // 将字符串中所有的’a’替换为’f’
s.split(" “); // 将字符串以空格作为分隔符，转化为字符串数组
s.substring(1); // 返回索引从1开始的字符串（索引从 0 开始）
s.substring(1， 4); // 返回从索引1开始，到4结束（不包括4）的字符串
s.tocharArray(); // 将字符串转化为字符数组
s.toLowerCase(); // 将字符串中的所有字符都转换为小写
s.toUpperCase(); // 将字符串中的所有字符都转换为大写
s.trim(); // 删除头尾空白
s.contains(“aa”); // 判断字符串中是否包含指定的字符或字符串
s.isEmpty(); // 判断字符串是否为空

ArrayList

List list = new ArraysList<>();

List list2 = new ArraysList<>();

list.add(“aaa”); // 直接添加元素

list.add(0, “aaa”); // 通过索引添加元素

list.addAll(list2); // 添加list2所有元素到list
List list3 = new ArraysList<>(Arrays.asList(“aaa”, “bbb”, “ccc”));
list.get(0); // 通过索引访问list中的元素
list.remove(2); // 通过索引删除list中的元素
list.clear(); // 清空list数组
list.size(); // 返回list中的元素个数
for / for-each // 遍历list
Collection.sort(list); // 对list进行排序
String[] arr = new String[list.size()];

list.toArray(arr); // 将list转化为数组

List list4= new ArrayList<>(Arrays.asList(arr)); //从数组创建ArrayList
list.toString(); // 将list转化为字符串
list.isEmpty(); // 判断list是否为空
list.contains(“aaa”); // 判断list中是否存在指定元素
list.indexOf(“aaa”); // 查找"aaa"的所在索引，不存在返回-1

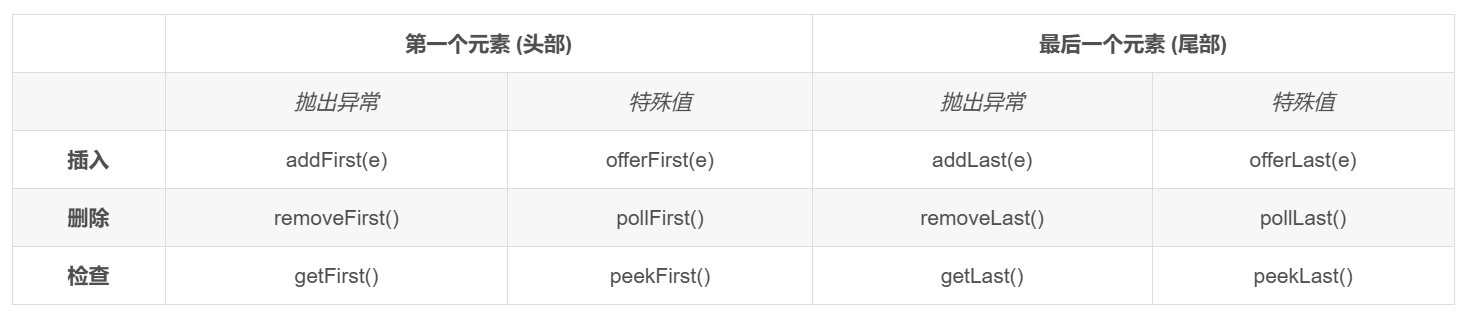
Deque

PriorityQueue（堆）

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35


// 创建小根堆
PriorityQueue<Integer> minHeap = new PriorityQueue<>((a, b) -> a - b);
// 加入数据
minHeap.offer(3);  // add
minHeap.offer(1);
minHeap.offer(4);
minHeap.offer(1);
minHeap.offer(5);
// 不断取出最小值
while(!minHeap.isEmpty()) {
    int cur = minHeap.poll(); // int
    System.out.println(cur + " ");
}

// 1 1 3 4 5

// 其他方法
minHeap.peek();
minHeap.remove(int x);  // boolean
// 遍历
Iterator<Integer> iterate = minHeap.iterator();
while(iterate.hasNext()) {
    System.out.print(iterate.next() + " ");
}
// 比较器
PriorityQueue<Integer> numbers = new PriorityQueue<>(new CustomComparator());

class CustomComparator implements Comparator<Integer> {
    @Override
    public int compare(Integer n1, Integer n2) {
        if(n1 > n2) return -1;
        else if(n1 < n2) return 1;
        else return 0;
    }
}

Arrays

Arrays.fill(arr, data); # 填充数组

Arrays.sort(); # 数组排序

1
2
3
4
5


Arrays.sort(int[][] arr, new Comparator<int[]>() {
    public int compare(int[] p1, int[] p2) {
        return p1[1]-p2[1];
    }
});

Arrays.toString(arr); # 将数组中的内容全部打印出来
Arrays.equals(arr1, arr2); # 比较数组元素是否相等
Arrays.binarySearch(arr, data); # 二分查找法找指定元素的下标
Arrays.copeOf(arr, len); # 截取数组

Arrays.copeOfRange(arr, left, right);

快排

归并

冒泡

二分